Jim Frankenfield - Papers[Technical] [Administrative] [Avalanche] [Web] |
[Papers] 
|
Pore-Space Characterization of Wet Snow in the Pendular Regime
Jim Frankenfield; 1338 Foothill Dr. #170, Salt Lake City, UT 84108
1-877-604-0166; snowman@csac.org
Abstract
The geometry of wetting fluid pendular rings in a porous media can be used to characterize the media in the unsaturatedpendular regime. A number of expressions for the volume and surface area of pendular rings in an ideal soil have been published but are not in agreement. A correct set of equations has been derived for an ideal soil of spheres and also for a sintered media represented by allowing the spheres to overlap. These volume and area expressions allow for the possibility of a non-zero contact angle between the wetting fluid and the solid.
The transition between the pendular and funicular regimes occurs when either the pendular rings merge or the capillary pressure (Pc) across the wetting/non-wetting interface becomes zero. Use of the Laplace Equation and the ring geometry leads to an implicit equation for the Pc=0 point. The roots of this equation are in general agreement with measured values of the transition saturation.
Characteristic curves of Pc vs. Saturation can be generated as well. The basis for this is the thermodynamic relation P=dE/dV. Energy can be calculated by using the interfacial area expressions and the related surface energies. Young's equation and symmetry can be used to reduce the necessary surface energies to only the wetting/non-wetting surface tension. A spreadsheet can then be used to generate the characteristic curves.
Volumes and Areas of Pendular Rings
Volume and area expressions for pendular rings around a point contact between two spherical particles (Fig 1) have been previously published. However, volume expressions given by Rose [1], Gardner and Gardner [2], Dallavalle [3] and Gvirtzman and Roberts [4] are found to differ.
The correct expression for the volume of such a ring with an arbitrary contact angle between the wetting fluid and the solid particle has been derived by Frankenfield [5] and is
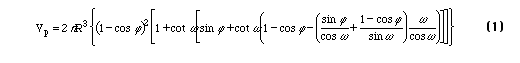
When the contact angle is zero this reduces to the result given by Rose [1]. The correct area for the wetting fluid - nonwetting fluid interface of such a ring was given by Gvirtzman and Roberts [4] and is
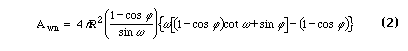
The area of the interface between the wetting fluid and the solid is
![]()
A somewhat more realistic approximation to the particle interface in wet snow is obtained by allowing it to flatten. Geometrically, this amounts to letting the two spheres in the ideal soil case overlap. (Figure 2) This is still a rough approximation. The nature of this interface is discussed in more detail by Colbeck [6]. For this geometry, Frankenfield [5] has shown that the correct volume and area expressions are
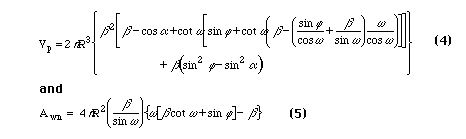
where b = cosa - cosj.
Maximum Pendular Ring Size (Transition to Funicular)
The pendular regime will end when the rings either merge or reach a size which creates a zero pressure difference across the wetting-nonwetting fluid interface.
When the pressure difference across the wetting-nonwetting interface becomes zero the rings can not become any larger. This pressure is given by the Laplace equation,
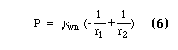
where gwn is the interfacial tension between the wetting and nonwetting fluids, so that r1 = r2 gives a condition for maximum ring size. This condition can be expressed in terms of ring size j and contact angle q;
![]()
where b = 1-cosj for the ideal medium and b = cosa - cosj for the flattened contact.
A good approximation in the ideal case is
![]()
Characteristic Curves
The capillary pressure across the wetting-nonwetting phase interface can be calculated by dividing the change in total surface energy by the change in volume, Pc = dE/dV .
Let's denote a surface tension or energy. The change in total surface energy is given by
![]()
Using Young's equation,
![]()
and the fact that DAws = -DAns the change in surface energy can be written as
The saturation can be calculated as the ratio of the volume of the rings contained in a unit cell to the volume of pore space in a unit cell. The resulting expression is
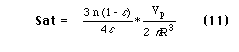
where e is the porosity and n is the number of spheres which each sphere touches, and is called the grain coordination number.
Capillary pressure as a function of saturation can now be graphed using a spreadsheet. The resulting curve will depend on the coordination number, the size of the flattened contact area, and the porosity. An example of such a curve is shown in Figure 3. Also shown, for comparison, is an empirical relation given by Colbeck [7]. The generated curve was adjusted to roughly approximate the empirical expression, but no effort was made to optimize the fit. Changing the model parameters may result in either a better or worse comparison.
References
- Walter Rose, J. Appl. Phys. 29, 687 (1958).
- Willard Gardner and John Hale Gardner, Soil Sci. 76, 135 (1953).
- J. M. Dallavalle, Micromeritics , 2nd ed. (Pittman, 1948), p.288.
- Haim Gvirtzman and Paul V. Roberts, Water Resour. Res. 27, 1167 (1991).
- Jim Frankenfield, self-published online, http://www.snowman-jim.org/papers/
- S.C. Colbeck, J. Colloid Interface Sci. 72, 371 (1979)
- S.C. Colbeck, Journal of Glaciology, Vol 13 #67, 1974
Figure Captions
Fig 1 - Definition of Parameters for a pendular ring about a point contact between two spherical soil or ice particles.
Fig 2 - Pendular ring about a flattened contact between two ice particles
Fig 3 - Theoretical characteristic curve. An empirical relation given by Colbeck is shown for comparison.

 Jim Frankenfield. |
[Papers] 
|